Formulas exist for the shear stiffness and largest shear stress in beams of many cross-section shapes. We started to check these formulas using 3D finite element analysis. It was found that the shear stiffness of square sections is much larger than the formula predicts. Formulas for round tubes were derived that include the wall thickness. Other cross-sections are being studied.

Thin wall beams are often much stiffer in torsion than a frame analysis program predicts. This is due to restrained warping at the beam-ends. The torsion theory of Vlasov takes this into account. We derived a simple manual method to include restrained warping in frame analysis. This can be particularly useful if a designed structure seems not to fulfil serviceability requirements.
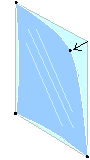
A rectangular panel that is twisted substantially will deform in an asymmetric way. We showed that this phenomenon can be reduced to a buckling problem. It was applied to derive formulas for designing curved glass fašades. For example, a vertex of a square panel can be displaced up to 16.8 times the thickness before asymmetric deformation occurs (Staak's formula). We also developed a special purpose finite element program for computing the stresses in cold bend glass panels.
Tent structures are prestressed to maintain their shape. We set out to find the optimal prestressing for a given shape. This is the counterpart of selecting the prestress and computing the shape, which is often used in tent design (form finding). As yet we were not able to develop a successful algorithm. The problem is finding suitable redundants. Even for very small tents this can take hours of computation time. The problem also occurs in applying the lower bound theorem of plasticity theory. So, a solution would find its way to many applications.

Hollow-core slab floors (kanaalplaatvloeren) often need to have large openings. These openings often can be made using simple trimmers (raveelijzers) without extra beams or columns. Design graphs cannot practically represent all possible opening positions and opening sizes for any floor geometry and loading. Therefore, there is a need for a special purpose finite element program for automated analysis of these floor systems.
We have identified critical locations in several floor systems with the finite element program KOLA. We derived analytical expressions for the stress state in the hollow-core slabs. The next step is to develop a pre and post processor for the analysis. The final program will run in real-time, have minimal input and minimal output. It will be especially suitable for a trial-and-error design process.
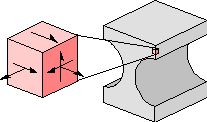
There are several procedures for designing reinforcement in concrete walls. However, sometimes we cannot apply such a procedure, for example if a building is renovated and the load on an existing wall will be increased. For this we developed a WWW program (Java applet) that computes cracking, material stresses and ultimate load of wall parts. An engineer needs to do a finite element analysis of the wall (linear) and he - or she - can use the applet to check the performance of critical parts. This is much faster than any alternative such as running a nonlinear finite element analysis or building a new wall.

Partial safety factors and load combinations in codes of practice are not valid for special projects with exceptional safety and durability requirements. For such a project the structural designers need to calculate safety factors and load combinations themselves. The theory and data to do so is often available but lacking is support of a user-friendly program.
Therefore, we are developing a simple tool for computation of safety factors and load combinations. An additional advantage of the program is that it does not use many of the approximations that are necessary in manual calculations.
Safety factors and load combinations can be used to compute the accompanying reliability. An algorithm has been developed, implemented and tested for this computation. The algorithm derives a response surface from the load combinations and computes its reliability. The structure itself is not used in this analysis.
The stringer-panel method is a way to model reinforced concrete walls for design purposes. Accurate and efficient stringer and panel element formulations have been derived and implemented. The program SPanCAD has been developed as a design tools. It includes linear and nonlinear analysis of statically loaded reinforced concrete walls. A successful design procedure has been developed. The program will be regularly upgraded to support new developments.

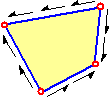
Shear panels are frequently used in structural models. Examples are aircraft wings, timber dwellings and reinforced concrete walls. Shear panels of rectangular and trapezoid shape have closed form stiffness matrices. However, the stiffness matrix of a quadrilateral (vierhoekig) shear panel needs to be approximated. We derived a mathematical formulation for this. The formulation shows to be accurate for any practical shape.
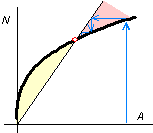
Designing a simple system can be based on trial and error, however, a complicated system requires a systematic approach. We studied design procedures for linear models, partially nonlinear models and highly nonlinear models. We also studied the convergence of design procedures based on optimality conditions including Picard iteration, secant iteration and Newton-Raphson iteration. It was confimed that it is best to use a simple model in the first step of a design procedure. It is planned to study design procedures based on reliability analysis.
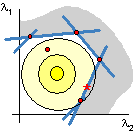
Calculation of safety factors often starts with approximated sensitivity factors (a-factors). Sensitivity factors are points in the space of design variables. For a safe system the convex hull of these points needs to enclose an n-sphere of radius 1. Therefore, the challenge is to find polytopes with small ratios of circumradius over inradius. Analytical and computational studies are ongoing. Recently, we found a remarkable result concerning the accuracy of structural analyses for few load combinations. One extra load case can be almost compensated by two exta load combinations.

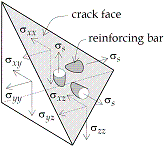
Software companies are extending their structural analysis programs with volume elements. Therefore, we developed a method for computing reinforcement requirements for three dimensional stress states. Clearly, this is an optimisation problem involving load combinations and performance requirements. Applying this method we found that in most designs the amount of reinforcement depends on crack control (serviceability limit state) and not on carrying capacity (ultimate limit state).